Bilanciare un gioco con il metodo dell’ancoraggio

Quello che state per leggere fa parte di una serie di articoli estratti dal mio lavoro “Progettare giochi da tavolo”. Si tratta di un progetto di cui ho parlato in questo post sul forum della Tana dei Goblin.

L’idea è quella di estrarre dai libri alcuni paragrafi che trattano argomenti ritenuti da me di particolare interesse e di presentarli sottoforma di articoli. Se avete già letto i libri non troverete nulla di nuovo, ma se non li aveste ancora letti potreste trovare qualche spunto interessante.

Di seguito gli articoli facenti parte di questa serie:
1 - Gli archi di gioco
2 - Progressione del gioco e dei giocatori
3 - Gestione dei pareggi
4 - La casualità come fonte di incertezza
5 - La tensione e la pressione
6 - Modellare la curva di apprendimento
7 - Bilanciare un gioco con il metodo dell’ancoraggio

La maggior parte dei giochi è basata su dei numeri, anche se spesso questi non vengono esposti direttamente ai giocatori. La matematica utilizzata per trovare questi numeri può essere più o meno spinta a seconda del gioco, ma indipendentemente da questo è bene che il designer la progetti dall’inizio utilizzando una specifica logica. Il metodo dell’ancoraggio, che vedremo in questo articolo, permette di fare proprio questo.

C’è da dire che cercando un equilibrio strettamente matematico difficilmente si riuscirà a trovare il bilanciamento finale del gioco. Tuttavia è consigliato senz’altro partire in questo modo nelle prime fasi di progettazione. Se si riesce a dare al gioco una buona impostazione matematica, infatti, esso avrà già da subito un bilanciamento che gli permetterà di essere giocabile. Nelle fasi successive, poi, sarà necessario fare degli aggiustamenti, delle limature o, come viene spesso chiamato, il bilanciamento fine. Ma intanto si avrà a disposizione già da subito un prototipo che sarà in grado di reggere le prime sessioni di playtest.

Un’ancora è un valore che può essere correlato direttamente con qualsiasi elemento presente nella parte di gioco che si intende bilanciare. Molte volte si tratta di un valore legato alla condizione di vittoria, alla condizione di sconfitta o al costo degli elementi. Per esempio, potrebbero essere punti vittoria, monete, punti vita o altri tipi di risorse. Una volta trovata l’ancora, tutti gli altri valori possono essere calcolati applicando una formula che va a definire una relazione con essa. 

Si prenda, ad esempio, un gioco in cui si debbano costruire degli edifici spendendo delle risorse. Supponiamo che esistano tre tipi di edifici, ognuno dei quali necessiti rispettivamente di 2, 3 e 4 risorse per essere costruito e che ognuno di essi conferisca un certo numero di punti vittoria. Inoltre, supponiamo esistano degli obbiettivi che richiedano di costruire tre edifici dello stesso tipo e che, come nel caso precedente, conferiscano dei punti vittoria. In questo esempio l’ancora può essere costituita dai punti vittoria, in quanto è un parametro che è in relazione diretta sia con gli edifici, sia con gli obiettivi. Supponiamo che il designer debba trovare dei valori bilanciati per i punti vittoria da assegnare sia agli edifici, sia agli obiettivi. Per farlo dovrà definire quali sono le relazioni tra questi e l’ancora. Ad esempio, potrebbe decidere che per gli edifici ogni risorsa spesa faccia guadagnare 2 punti vittoria, ottenendo il risultato illustrato nella seguente tabella. 

Per gli obiettivi, invece, potrebbe decidere che ogni risorsa spesa per costruire i tre edifici richiesti faccia guadagnare 1 punto vittoria. La seguente tabella illustra il risultato.

Con questo procedimento si è potuto ottenere degli edifici e degli obiettivi bilanciati tra di loro. Sarebbe stato possibile anche applicare un procedimento inverso, ovvero partire dai punti vittoria che si voleva assegnare agli edifici e agli obiettivi per, poi, trovare il numero di risorse richieste.

In questo esempio è stata presa in considerazione solamente una parte del gioco senza specificare come questi elementi siano integrati con il resto. Potrebbe accadere, quindi, che nel momento in cui si va a provare il gioco, il bilanciamento trovato si dimostri non adeguato rispetto alla parte di gioco non presa in considerazione. Nell’eventualità si può provare a cambiare i valori delle relazioni per fare in modo che il bilanciamento degli edifici e degli obiettivi si adatti meglio al resto del gioco. Ad esempio, si potrebbe decidere che per gli edifici ogni risorsa spesa faccia guadagnare 3 punti vittoria invece di 2 e per gli obiettivi 2 punti vittoria invece di 1. 

Molte volte, nella realtà si avrà a che fare con degli scenari più complessi rispetto a questo. Potrebbe essere necessario, ad esempio, tenere conto del numero di risorse presenti, di come queste vengono raccolte, del fatto che alcune di esse potrebbero essere più rare di altre o del fatto che alcune potrebbero essere usate anche per altri scopi all’interno del gioco. Sebbene tutti questi parametri possano complicare i conteggi da fare, il procedimento legato all’ancoraggio rimane comunque lo stesso.

Le cose si complicano un po’ quando si devono bilanciare dei parametri che non sono direttamente quantificabili come, ad esempio, abilità, azioni, poteri speciali, meccaniche o altro. Per esempio, come fa il designer a bilanciare i valori di due carte che permettono di fare azioni diverse nel gioco? Come fa a bilanciare delle caratteristiche uniche assegnate ai personaggi presenti nel gioco? Come fa a bilanciare dei poteri speciali che vengono dati come bonus? La difficoltà consiste nel fatto che ci si trova a dover valutare e bilanciare delle caratteristiche che non sono direttamente confrontabili tra di loro. In questi casi il designer non può fare altro che fare una stima di quanto possano valere le varie caratteristiche presenti, per poi verificarne la correttezza attraverso dei playtest ed eventualmente correggere il tiro. 

Si supponga, per esempio, che si debba calcolare il costo di due navicelle spaziali che differiscono solamente per una caratteristica: la prima ha in dotazione l’invisibilità, mentre la seconda è il doppio più veloce dell’altra. Il designer dovrà iniziare facendo una stima di quanto possano valere queste due caratteristiche nel contesto del gioco e assegnargli un valore numerico. I valori ottenuti, poi, dovranno essere messi in relazione con il costo in monete, che supponiamo essere l’ancora. Infine, tramite una serie di playtest, dovrà valutare la correttezza della stima fatta, apportando eventualmente dei correttivi. Supponiamo che il designer stimi, su una scala da 1 a 10, un valore di 5 per l’invisibilità e un valore di 6 per la velocità. Definisce, poi, la seguente relazione con il costo: ogni navicella spaziale costerà 50 monete come costo base, al quale andranno aggiunte 5 monete moltiplicate per il valore della caratteristica speciale. Si otterrà, così, un valore di 75 (ovvero 50 + (5 x 5)) per la prima navicella e un valore di 80 (ovvero 50 + (5 x 6)) per la seconda. A seguito di una serie di playtest, però, il designer si accorge che la velocità è molto più forte di quello che aveva immaginato, così decide di alzare il valore di questa caratteristica da 6 a 8, ottenendo un costo di 90 (ovvero 50 + (5 x 8)). Questa modifica dovrà, a sua volta, essere verificata da altri playtest che potranno confermala oppure suggerire altri cambiamenti. 

In alcune occasioni ci si trova a dover bilanciare degli elementi complessi ai quali fanno capo una serie di caratteristiche. Si prenda, per esempio, un gioco asimmetrico in cui i partecipanti devono scegliere una fazione da usare durante la partita. Tipicamente, in questi casi, ognuna delle fazioni avrà un insieme di caratteristiche diverse. Per esempio, una potrà essere forte in attacco e debole in difesa, un'altra potrà essere forte in difesa ma lenta nel movimento e così via. Il designer avrà il compito di fare in modo che tutte le fazioni abbiamo le stesse possibilità di vittoria e che non ce ne siano alcune più forti di altre. In sostanza dovrà fare in modo che le caratteristiche di ogni fazione prese nel loro insieme siano bilanciate se confrontate tra di loro. 

In casi di questo tipo è possibile utilizzare la tecnica dell’ancoraggio comparativo. Si tratta di stabilire per ogni caratteristica del componente di gioco da bilanciare (le fazioni dell’esempio precedente) un numero che vada a indicare il vantaggio che conferisce, sommare questi valori e usare il risultato come ancora. A quel punto si può bilanciare i vari elementi comparando le ancore (ovvero le somme): andando a modificare le caratteristiche dei vari elementi si dovrà fare in modo che le ancore siano tutte uguali o per lo meno che abbiano dei valori simili.

Tornando all’esempio precedente, si supponga che ogni fazione abbia quattro parametri diversi: attacco, difesa, movimento e magia. Per ognuno di questi parametri il designer crea tre opzioni, come illustrato nella seguente tabella.

Supponiamo che il designer definisca inizialmente la seguente distribuzione di dotazione tra le tre fazioni in gioco.

Il compito del designer è quello di verificare che nel loro complesso le fazioni siano bilanciate e di correggere eventuali squilibri.

Per prima cosa è necessario riuscire ad associare a tutte le dotazioni dei numeri che rappresentino il livello di vantaggio conferito al giocatore che le possiede. I valori dovranno avere la stessa scala numerica in modo che siano confrontabili tra di loro. Come si può immaginare questo è già un primo scoglio da superare, in quanto i singoli parametri possono non essere facilmente rappresentabili con dei numeri. Ad esempio, si può essere consapevoli che un’arma è più forte di un’altra, ma riuscire a quantificarne la forza con dei valori può essere complicato. Inoltre, potrebbe non essere facile nemmeno trovare il modo di calcolare un valore che sia confrontabile tra i diversi ambiti. Per esempio, un valore 5 in attacco deve corrispondere allo stesso livello di vantaggio di avere un valore 5 in movimento. Nonostante queste difficoltà, il designer deve provare a identificare dei valori sensati che gli permettano di iniziare l’attività di bilanciamento.

Supponiamo che, doppo un’attenta analisi, il designer abbia assegnato un valore, in un intervallo da 1 a 5, a ogni dotazione possibile. La seguente tabella ne mostra il risultato.

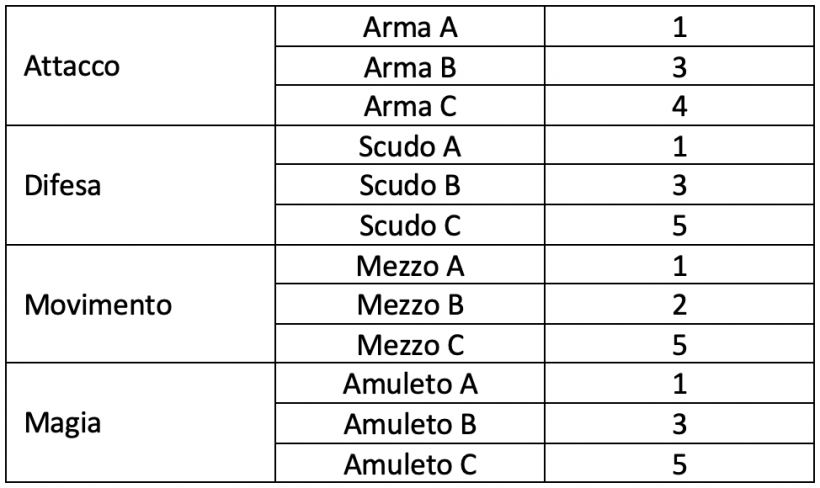
In base a questi numeri è possibile assegnare un valore a ogni dotazione assegnata alle tre fazioni e calcolarne la somma.

Da una prima occhiata alla tabella sembra che la fazione 2, avendo un insieme di dotazioni che producono una somma inferiore alle altre, sia in svantaggio. Le altre due, invece, sembrano bilanciate tra di loro. Arrivati a questo punto, prima di procedere oltre, è necessario verificare che la situazione sia realmente come quella illustrata nella tabella. Attraverso una serie di playtest, infatti, sarà necessario accertarsi che i valori ipotizzati per ognuna delle dotazioni corrispondano alla situazione reale.

Si supponga che, a seguito di alcune prove, la Fazione 2 sembri effettivamente più debole, ma non di molto, mentre le altre due sembrino alla pari. Inoltre, sempre dai test, sembra emergere che il Mezzo C sia più debole di quanto ipotizzato e quindi si decide di abbassarne il valore da 5 a 3. Aggiornando il valore del Mezzo C nella tabella, si ottiene quanto segue.

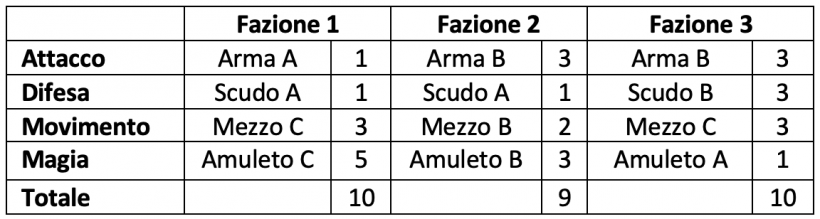
A seguito di questo aggiustamento si sono ridimensionati i valori totali delle Fazioni 1 e 3. La Fazione 2 resta svantaggiata, ma la differenza con le altre è minore di quella che risultava precedentemente, proprio come è emerso dai playtest. A questo punto, per bilanciare la Fazione 2 con le altre è necessario sostituire una delle sue dotazioni con una più forte in modo da aumentare il suo valore totale di un punto. Si decide, quindi, di sostituire l’Arma B con l’Arma C, ottenendo il seguente risultato.

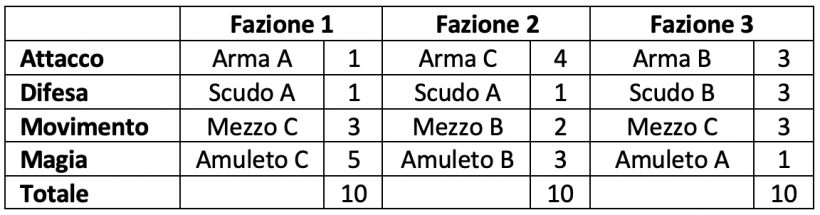
Ora le tre Fazioni sembrano matematicamente equilibrate. Sarà comunque necessario eseguire dei playtest per accertarsi che l’esperienza di gioco confermi questa ipotesi.