
Articolone. Inchino.

Oggi abbiamo scomodato nientemeno che Dario De Toffoli, che ci ha scritto questo splendido articolo sulla matematica e i giochi da tavolo.
Agzaroth
Giocate a Catan e state facendo il piazzamento iniziale, che poi è la mossa chiave che influenzerà tutta la partita. La prima cosa che guardate è il numero sui territori, perché più quel numero è vicino a 7, più è probabile che esca: il 6 e l’8 escono 5 volte su 36, il 5 e il 9 escono 4 volte su 36 e così via fino al 2 e al 12 che hanno una sola probabilità su 36. Non se ne scappa, se si lanciano due dadi un po’ di matematica fa capolino.
E prima di Catan, quando giocavate a Risiko!, chiaramente chi attaccava troppo tendeva a perdere sistematicamente, magari non si rendeva conto che attaccando 3 contro 3 armate se ne perdono in media 1,89 per colpo… e anche questa è matematica.
Ma ci sono mille altri modi in cui la nostra amica matematica fa capolino in un gioco.
In Rasende Roboter per esempio si tratta della minimizzazione i percorsi… quanti ricordi, mi vengono in mente i tempi in cui giocavo con Alex Randolph mentre lo stava mettendo a punto: troppo divertente batterlo!
Questione di percorsi da ottimizzare, seppur in modo assai diverso, anche in Cartagena di Leo Colovini; a proposito, nel primo prototipo si trattava di raggiungere numeri, gli oggetti pirateschi sono stati aggiunti in fase di rifinitura.
E Dr. Eureka di Roberto Fraga? Appena l’ho visto mi è parsa evidente l’intelligente derivazione del rompicapo matematico noto come Torre di Hanoi: come non averci pensato prima?
Che dire poi di Acquire di Sid Sackson, altro grandissimo classico che a mio avviso è un po’ sottovalutato dai moderni gamers. Bisogna fare sempre estrema attenzione al numero di azioni di una certa compagnia che sono in giro; per esempio si è scatenata la corsa alle Fusion, due avversari ne hanno entrambi 7 e ora tocca a voi che ne avete 4: potete scalare la compagnia? No, in nessun caso. Se voi ne comperate altre 3, arrivate a 7 e ne restano 4 da acquistare (in totale sono 25); il primo avversario ne compererà certamente 3 e sarà il primo con 10, il secondo avversario compererà l'ultima e sarà secondo con 8… a voi le sole pive nel sacco.
Insomma, sotto sotto, se si va ad analizzare attentamente, sono veramente tanti i giochi che poggiano su un solido impianto matematico, anche se spesso i giocatori non stanno troppo a pensarci.
Certo, in alcuni casi è più evidente, come nel bellissimo Hare&Tortoise (per gli amici “Carotine”) di David Parlett, che nel 1979 è stato in assoluto il 1° Spiel des Jahres: se non lo avete mai giocato, non ditelo a nessuno e colmate la lacuna! Qui le regole complete.
Vediamolo comunque un po’ più da vicino.
Si parte dalla casella 64 e bisogna scendere fino alla casella O (zero), il traguardo.
Per muoversi si spendono carote, delle quali si riceve una dotazione iniziale di 65 carote che sarà possibile integrare durante il percorso.
Il bello è che al proprio turno uno si muove quanto vuole, fino a una qualsiasi casella libera. Però più si muove, più carote paga: 1 passo = 1 carota; 2 passi = 3 carote; 3 passi = 6 carote... insomma ogni ulteriore passo costa una carota in più del precedente, secondo la seguente tabella:
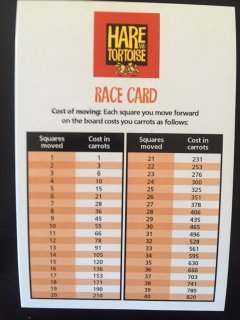
Quello che succede dopo la mossa dipende dalla casella in cui si arriva, come spiegato nelle regole.
Vince chi raggiunge il traguardo, ma per poterlo attraversare per primo bisogna avere non più di 10 carote in mano.
Senza scendere in dettagli strategici, vediamo un esempio di ottimizzazione nel finale.
Sei nella casella 21, ti sei già liberato di tutte le lattughe e sei in testa, al momento non raggiungibile. Hai in mano 145, come puoi finire in due mosse?

Un passo da 10 e uno da 11 non vanno bene, perché consumeresti solo 121 carote, lasciandone troppe (24) in mano. Nemmeno funzionano le coppie 9/12, 8/13 e 7/14. Funziona invece un passo da 6 e uno da 15, però bisogna fare prima quello da 6, perché altrimenti si finisce sulla lepre. L'altra possibilità è fare un passo da 16, per arrivare alla casella 4 e restare con 9 carote. Si riparte guadagnandone 10, che si spendono per tagliare il traguardo con 9.
Poi ci sono i giochi di numeri, basati proprio sul calcolo.
Contiamo ad esempio è un gioco di calcolo con semplici regole: dati sei numeri e operando su di essi con le sole quattro operazioni aritmetiche, si tratta di raggiungere (o avvicinarsi il più possibile) a un numero-obiettivo di tre cifre; ogni numero può essere usato una sola volta. Non si è infine obbligati a usare tutti e sei i numeri, anzi meno numeri si adoperano migliore viene considerata la soluzione. Naturalmente possono essere riutilizzati i risultati parziali che via via si ottengono.
Consideriamo per esempio il problema proposto in figura:
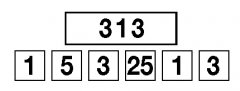
Vuol dire che si tratta di raggiungere 313 operando a partire dai numeri 1-5-3-25-1-9.
Ci si può riuscire utilizzando tutti e sei i numeri: 25+5=30; 30+1=31; 9+1=10; 31x10=310; 310+3=313. Ma ci si può riuscire anche utilizzando solo 5 dei 6 numeri, infatti: 25+1=26; 9+3=12; 26x12=312; 312+1=313 e il 5 rimane inutilizzato.
Contiamo nasce dal gioco televisivo Paroliamo e Contiamo, ideato in Francia da Armand Jammot col nome Des chiffres et des lettres. Per risolvere problemi di Contiamo i concorrenti avevano 45 secondi circa. Nel 1985 Adica Pongo ha commercializzato una versione in scatola del gioco.
Un gioco da tavolo basato su simili procedimenti aritmetici, ma assai più articolato, è Nubble, purtroppo non distribuito in Italia.

Si lanciano 4 dadi e si combinano i risultati con le 4 operazioni, per conquistare uno dei numeri ancora liberi sul tavoliere: più alto il numero ottenuto, maggiore il punteggio.
Ma c’è un concetto matematico più profondo che troviamo in alcuni giochi classici, quello di “Speranza matematica”. Proviamo a capire come funziona.
Giochiamo a Testa o Croce, una chip al colpo: quando vinco, guadagno una chip, quando perdo ci rimetto una chip. Dato che a ogni colpo ho il 50% di probabilità di vittoria, alla lunga il mio risultato tenderà al pareggio. Semplice e intuitivo. Si dice che il gioco è equo, il suo rendimento (o speranza matematica) è pari a 1.
Passiamo alla Roulette e puntiamo un gettone su un Pieno. La probabilità di vittoria è 1 su 37 e dunque il premio equo dovrebbe essere 37 gettoni (compreso il gettone puntato); il casinò invece ritorna 36 volte la posta e la differenza è la sua trattenuta, pari a circa il 2,70%. Il rendimento è dunque pari ai 36/37 del premio equo, il che corrisponde al 97,30%: in questo caso il gioco è svantaggioso, ogni volta che gioco perdo in media il 2,70% di quanto puntato.
Tutti i giochi che si fanno contro la “casa” sono svantaggiosi.
Dunque la speranza matematica (o equity), può essere definita come la speranza di vittoria di una data situazione, cioè il suo valore teorico; io prendo una situazione e la gioco infinite volte: il mio guadagno medio per gioco è proprio l'equity di quella situazione. E si tratta di un guadagno positivo se sono favorito, di un guadagno negativo (una perdita, in sostanza) se sono sfavorito.
Ma vediamo come questo concetto viene declinato nei grandi classici.
Partiamo dal Backgammon, un gioco che per molti anni è stato al centro dei miei interessi, perfetta miscela di abilità e fortuna. È un gioco di ottimizzazione probabilistica, cioè c’è un motore aleatorio e i giocatori devono sempre cercare la mossa migliore nelle situazioni più o meno casuali che si trovano ad affrontare. Chi prende le decisioni migliori, alla lunga, vince.
Chi conosce le regole del Backgammon non ha bisogno di spiegazioni: per chi non le conosce, data la semplicità della posizione, poche note dovrebbero bastare.
La cosa importante è che il giocatore di turno, prima di tirare i 2 dadi, ha la possibilità di proporre all'avversario il raddoppio della posta: se questi accetta la posta in palio viene raddoppiata, se rifiuta la partita termina subito e il giocatore incassa subito la posta singola. La cosa interessante è che se a un giocatore conviene offrire il raddoppio (perché ritiene di essere favorito nella vittoria finale), non è affatto detto che al suo avversario convenga rifiutarlo. Potrebbe sembrare una contraddizione, ma in realtà in molti casi avviene proprio il contrario. Non è un paradosso. Chiaramente per chi si trova in svantaggio la cosa migliore sarebbe che il raddoppio non gli venisse offerto, ma a proposta fatta l'accettazione è spesso il minore dei mali. Chiariamo il concetto con un esempio.
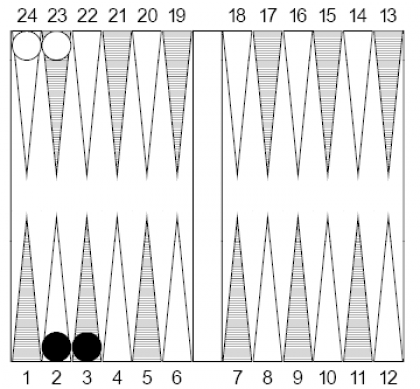
Tocca il Nero: deve raddoppiare? Il Bianco, se raddoppiato, deve accettare o passare?
Siamo in un finale di partita e sia il Nero che il Bianco hanno ancora 2 pedine da togliere dal tavoliere. Tocca al Nero, che per vincere deve toglierle entrambe in un tiro (in caso contrario il Bianco vincerebbe con qualsiasi tiro). Per ottenere questo risultato bisogna semplicemente che nessuno dei due dadi che lancia contenga un 1: le probabilità sono a suo favore, infatti riuscirà nell'intento in 25 dei 36 possibili esiti del lancio di 2 dadi (nei restanti 11 almeno un dado conterrà un 1 e il Nero perderà). Consideriamo le varie possibilità.
Giocando 36 volte questa situazione il Nero ne trarrà un guadagno statistico medio di 14 punti, infatti vincerà 25 volte e perderà 11 volte: + 25 (punti vinti) – 11 (punti persi) = + 14 (guadagno).
14 punti su 36 partite corrispondono a un guadagno netto medio di 0,39 punti per partita. Si può dire che non raddoppiando, la sua equity o speranza di vittoria o valore teorico della sua posizione è +0,39 (attenzione, stiamo parlando di punti, non di percentuali).
Il Nero guadagna 1 punto per partita (36 punti per 36 partite) e la sua equity sale a +1,00.
Ora le probabilità di vittoria sono le stesse del caso del non raddoppio, ma il guadagno sarà raddoppiato, proprio a causa del raddoppio dei punti in palio; dunque su 36 partite il Nero vincerà 25x2=50 punti e ne perderà 11x2=22, per un guadagno netto di 28 punti, pari a una media di 0,78 punti a partita.
Riassumiamo i tre casi possibili:
| N non raddoppia | +0,39 punti a partita |
| N raddoppia e B passa | +1,00 punti a partita |
| N raddoppia e B prende | +0,78 punti a partita |
In una simile situazione il raddoppio è di rigore: se l’avversario rifiuta il Nero porterà a casa il suo punto senza fiatare, se accetta il suo guadagno statistico raddoppierà essendo raddoppiata la posta in palio.
Mettiamoci ora dalla parte del Bianco, che certo non è entusiasta della situazione e si trova costretto a operare una scelta fra una sconfitta sicura, ma singola e una sconfitta probabile, ma doppia. Giocando 36 volte, se rifiuta la sua perdita sarà di un punto a partita per un totale di – 36 punti; se invece accetta perderà 0,78 punti a partita, per un totale di 28 punti (tanti quanti ne vincerebbe il Nero). È evidente che in questa situazione il Bianco alla lunga perderà in ogni caso; quello che deve fare però è minimizzare la perdita: meglio trovarsi a – 28 piuttosto che a – 36 o, in altre parole, meglio perdere una media di 28/36 di punto a partita, piuttosto che un punto intero.
In definitiva, anche con meno di 1/3 di probabilità di vittoria conviene accettare il raddoppio. Ma qual è il limite di probabilità sotto il quale bisogna rifiutare? Quello corrispondente ad una perdita statistica media di 1 punto a partita cioè, a conti fatti, il 25%. Quando si ha il 25% di possibilità di vittoria accettare o rifiutare il dado è indifferente.
Consideriamo ad esempio la situazione seguente.

Tocca il Nero: deve raddoppiare? Il Bianco, se raddoppiato, deve accettare o passare?
Tocca al Nero che per vincere deve togliere l'ultima sua pedina in questo tiro: ci riuscirà se la somma dei due dadi sarà pari almeno a 6 (o anche se i dadi sono 2-2). Fra le 36 possibilità questa volta i tiri positivi sono 27 e solo 9 quelli negativi (1-1, 1-2, 2-1, 1-3, 3-1, 1-4, 4-1, 2-3, 3-2), dunque chiaramente il Nero raddoppia. Il Bianco con le sue 9 chance su 36 (25%) se rifiuta avrà un saldo statistico negativo di – 36; se accetta il saldo sarà lo stesso, infatti: 9x2 (punti vinti) – 27x2 (punti persi) = -36 (perdita). Il 25% è dunque il punto di equilibrio.
Le valutazioni fatte per il Backgammon sono utilissime per capire il metodo da applicare – con gli opportuni adattamenti – anche a moltissime situazioni di Poker.
Si tratta di situazioni in cui la parte di valutazione psicologica è ormai passata e le probabilità di vittoria dipendono ormai sostanzialmente solo dal river (o dal turn e dal river); dunque la decisione di vedere o meno è legata alla probabilità di uscita di una carta positiva (che bisogna imparare a calcolare velocemente e correttamente) e all'entità del piatto in gioco. Quando un giocatore sta pensando se “vedere” o meno, sta in realtà – più o meno consciamente – valutando la sua speranza matematica; sta pensando a cosa succederebbe se si trovasse a giocare quella stessa situazione infinite volte: alla lunga ci guadagnerebbe o ci perderebbe? Proprio come succedeva a backgammon: meglio darlo o non darlo il dado del raddoppio? Meglio accettarlo o rifiutarlo? E come si fa a prendere la decisione corretta? Beh, anzitutto bisogna porsi le 3 domande di rito, trovare le risposte esatte e metterle in relazione tra loro in un tempo ragionevole.
Queste sono le 3 domande che bisognerebbe sempre porsi per decidere se giocare o meno una mano. In altre parole si tratta di valutare quelle che molti chiamano pot odds.
Naturalmente alla terza domanda spesso non si può rispondere che con una stima, ma normalmente una stima è quanto basta per un giudizio sufficientemente accurato.
Consideriamo ora 3 piccoli esempi, con 2 soli giocatori e supponendo note le probabilità di vittoria.
| pot: | 75 |
| puntata: | 25 |
| prob. di vittoria: | 50% |
Mi conviene vedere? Ma certo! Infatti rischio alla pari 25 per guadagnare 75. Giocando all’infinito questa scommessa avrei un guadagno netto di 25 per ogni giocata (esattamente +75 ogni volta che vinco, -25 ogni volta che perdo) e per quanto possa essere grossolana la stima delle possibilità di vittoria, è chiara la convenienza della scommessa.
| pot: | 100 |
| puntata: | 50 |
| prob. di vittoria: | 25% |
Mi conviene vedere? In questo caso vincerei 100 una volta su quattro e perderei 50 tre volte su quattro, per un totale di +100-(50x3)=-50 ogni 4 mani, cioè -12,5 ogni mano: chiaramente mi conviene passare.
| pot: | 150 |
| puntata: | 50 |
| prob. di vittoria: | 30% |
Mi conviene vedere? In questo caso su 10 volte ne vincerei 3 (incassando un totale di 150x3=450) e ne perderei 7 (per un totale di 50x7=350): dunque avrei un guadagno di 450-350=100 in 10 mani, pari ad una media di 10 per mano. Un guadagno modesto, ma che dimostra come la dimensione del pot rende conveniente giocare anche in situazioni dove si è nettamente sfavoriti.
In conclusione voglio solo far notare che questi accenni alla speranza matematica non esauriscono neanche lontanamente l’interessantissima matematica che si cela dietro alcuni dei grandi classici, quali appunto sono Backgammon e Poker.
Non ci sono a mio avviso – non arrabbiatevi – giochi da tavolo moderni che possano reggere il confronto.
Dario De Toffoli, Venezia, 1 marzo 2017

Articolone. Inchino.
Molto interessante, davvero questo articolo sintetizza come mai io non mi sia mai messo a creare giochi miei. Serve una buona base matematica e quindi io sono fuori :)
Complimenti per l'articolo!
Mi professo del tutto incapace di stare al passo con il ragionamento matematico "serio", poiché si tratta di una materia in cui ho sempre faticato.
Tuttavia, gli argomenti sopra esposti mi affascinano.
Ciao,
Paolo (MPAC71)
I miei complimenti all'autore, bell'articolo!
Bellissimo articolo, specialmente per chi come me di matematica è appassionato. Complimenti!
eh si! è proprio bello questo articolo ed evocativo... mio padre me lo diceva sempre quando studiavo matematica a scuola :" fare i compiti di matematica è divertente come fare la settimana enigmistica" e aveva ragione!
m@
Bello...bell'articolo...
mi sto avventurando nella creazione di giochi da tavolo e ogni volta arrivo al punto in cui bisogna fare i conti con le probabilità di accadimento di situazioni, concomitanza di costi e quant'altro..e tutto ha decisamente a che fare con principi matematici..
il bello è quando un gioco riesce a nascondere l'impatto della matematica agli occhi di chi gioca!
"Giochiamo a Testa o Croce, una chip al colpo: quando vinco, guadagno una chip, quando perdo ci rimetto una chip. Dato che a ogni colpo ho il 50% di probabilità di vittoria, alla lunga il mio risultato tenderà al pareggio. Semplice e intuitivo. Si dice che il gioco è equo, il suo rendimento (o speranza matematica) è pari a 1."
Il valore atteso in questo caso è 0, non 1. D'altronde, se l'EV non fosse 0, non potrebbe essere definito gioco equo. ;)
"Giochiamo a Testa o Croce, una chip al colpo: quando vinco, guadagno una chip, quando perdo ci rimetto una chip. Dato che a ogni colpo ho il 50% di probabilità di vittoria, alla lunga il mio risultato tenderà al pareggio. Semplice e intuitivo. Si dice che il gioco è equo, il suo rendimento (o speranza matematica) è pari a 1."
Il valore atteso in questo caso è 0, non 1. D'altronde, se l'EV non fosse 0, non potrebbe essere definito gioco equo. ;)
grazie Galandil, corretto nel testo.
affascinante!
Fantastico, ma daltronde Dario ha una testa unica ( e me ne accorsi ai Campionati Italiani giocandoci contro a Rummikub... un bgno di sangue).
@galandil: Dario ha detto che è corretto 1. Sta recuperando la sua password e poi ti risponde.
L'articolo è molto molto interessante.
inoltre è intrigante notare che una buona parte degli esempi riguardano giochi d'azzardo (roulette, backgammon e poker), e che in un modo o in un altro hanno a che fare con posta, rilancio e la scommessa in generale.
sarebbe molto stimolante sapere che ne pensa De Toffoli sul perchè i nostri giochi da tavolo "moderni" preferiti hanno abbandonato questo tipo di meccaniche per arrivare ad un determinismo più spinto e a molto meno azzardo, anche alla luce dell'ultima frase dell'articolo :)
@galandil: Dario ha detto che è corretto 1. Sta recuperando la sua password e poi ti risponde.
è corretto 1, perchè il rendimento è quanto ti torna dopo aver investito inizialmente 1, quindi risulta equo se non hai alcun guadagno. Di contro, 0 è il valore atteso del guadagno.
Articolo molto bello! sarebbe da approfondire trattando anche approfonditamente dei giochi meno tradizionali!
Galandil capisco quello che intendi… ma la speranza matematica dell'esempio di testa e croce è 1 e non 0.
Giocando 1 quando si vince si vince 2, quando si perde si vince 0, il valore atteso è quindi 1, esattamente quanto si punta e dunque alla lunga si va in pari.
Se fosse 0, non si vincerebbe mai e si perderebbe 1 a ogni colpo.
In percentuale il rendimento è del 100%, cioè il gioco è equo.
Vedi anche: https://it.wikipedia.org/wiki/Valore_atteso
Per riassumere il concetto:
RENDIMENTO
R = PxN (R=rendimento, P=probabilità, N=numero di poste che si incassano)
TESTA O CROCE
P=0,5
N=2
R=0,5x2=1
R=1 gioco EQUO
R<1 gioco SVANTAGGIOSO
R>1 gioco VANTAGGIOSO
L'articolo è molto molto interessante.
inoltre è intrigante notare che una buona parte degli esempi riguardano giochi d'azzardo (roulette, backgammon e poker), e che in un modo o in un altro hanno a che fare con posta, rilancio e la scommessa in generale.
sarebbe molto stimolante sapere che ne pensa De Toffoli sul perchè i nostri giochi da tavolo "moderni" preferiti hanno abbandonato questo tipo di meccaniche per arrivare ad un determinismo più spinto e a molto meno azzardo, anche alla luce dell'ultima frase dell'articolo :)
Non so bene che cosa intendi per "moderni", ma direi che alcuni dei migliori giochi da tavolo (a cominciare da Catan) non siano deterministici; c'è un motore aleatorio e il giocatore deve sempre ottimizzare dalla situazione che si ritrova a gestire. Comunque oggi ci sono giochi davvero per tutti i gusti.
Separerei poi i giochi con componente aleatoria ma il cui esito dipende dalle scelte del giocatore (tipo Catan, backgammon o poker) da quelli propriamente d'azzardo in cui il giocatore non è coinvolto nell'esito della partita (tipo roulette).
Articolo moooolto interessante! Grazie!
Che meraviglia, complimenti :)
@diderot:
No, la speranza matematica (o valore atteso, sono due modi di chiamare la stessa cosa) è 0 nel tuo esempio.
Nel tuo commento, hai scritto: "Giocando 1 quando si vince si vince 2, quando si perde si vince 0, il valore atteso è quindi 1, esattamente quanto si punta e dunque alla lunga si va in pari.", e stai commettendo l'errore di non aggiungere all'equazione il costo di 1 (ergo -1) il 100% delle volte ad ogni lancio di moneta.
Questo perché il valore atteso DEVE comprendere per definizione l'eventuale costo per giocare (che è un evento a probabilità 1).
In formule, ed usando la tua notazione sempre del commento:
P(testa) = P(croce) = 0.5
N(testa) = 1, N(croce) = -1
EV = N(testa)xP(testa) + N(croce)xP(croce) = 1x0.5 + (-1)x0.5 = 0
Separando invece l'evento "giocata" dai risultati di testa e croce, l'equazione è:
P(testa) = P(croce) = 0.5, P(giocata) = 1
N(testa) = 2, N(croce) = 0, N(giocata) = -1
EV = N(testa)xP(testa) + N(croce)xP(croce) + N(giocata)xP(giocata) = 2x0.5 + 0x0.5 + (-1)x1 = 0
Non esiste un concetto di speranza matematica diversa dal valore atteso, sono la stessa cosa. E la definizione di gioco equo è EV del gioco = 0 (qui c'è la spiegazione molto semplice con un esempio in formula: http://www.ripmat.it/mate/l/ld/ldca.html ).
Di contro, 0 è il valore atteso del guadagno.
Giusto per la precisione: valore atteso *del guadagno* non ha proprio alcun senso come frase. Il valore atteso E' un guadagno SE è positivo, ma il valore atteso di per se viene valutato ad ogni possibile istante di scelta (compreso il giocare o non giocare) in un gioco, non su un guadagno.
galandil, il guadagno è definito come ricavi-costi, quindi posso benissimo farne il valore atteso, dato che è funzione di ricavi.
ad ogni modo, ben sapendo che sei bravo a discutere, la termino qua ;)
Per scrivere un commento devi avere un account. Clicca qui per iscriverti o accedere al sito
Accedi al sito per commentare© 2004 - 2023 Associazione Culturale - "TdG" La Tana dei Goblin
C.F./P.IVA: 12082231007 - P.le Clodio 8, 00195 Roma
Regolamento del sito | Archivio | Informativa privacy e cookie | Contatti
La Tana dei Goblin protegge e condivide i contenuti del sito in base alla seguente licenza Creative Commons: Attribuzione - Non Commerciale - Condividi allo stesso modo, v.4.0. Leggi il testo sintetico, oppure il testo legale della licenza.